Notebook Iris Dataset

Before we dive in, here’s a quick summary: the dataset contains 150 samples of iris flowers, each characterized by four features: Sepal Length, Sepal Width, Petal Length, and Petal Width, all measured in centimeters. These samples are grouped into three species: Setosa, Versicolor, and Virginica. If you’re not familiar with the dataset, you can learn more about it here.

1 Loading the dataset

Let’s start by importing the iris dataset and manipulating the dataframe so that the column names match the feature names.

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import pandas as pd 

# Load toy dataset
iris = load_iris() 
 # Create dataframe using feature names
df = pd.DataFrame(iris.data, columns=iris.feature_names)

2 Exploring the dataset

Let´s start by exploring the species by plotting the sepal length vs. width in a scatter plot

import matplotlib.pyplot as plt

_, ax = plt.subplots()
scatter = ax.scatter(iris.data[:, 0], iris.data[:, 1], c=iris.target)
ax.set(xlabel=iris.feature_names[0], ylabel=iris.feature_names[1])
_ = ax.legend(
    scatter.legend_elements()[0], iris.target_names, loc="lower right", title="Classes"
)

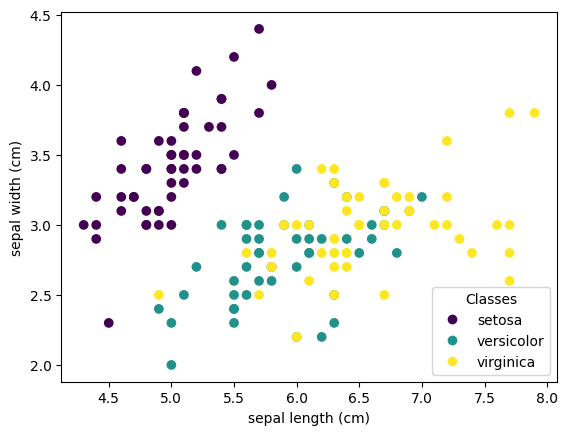
You can already see a pattern regarding the Setosa type, which is easily identifiable based on its short and wide sepal. Only considering these 2 dimensions, sepal width and length, there’s still overlap between the Versicolor and Virginica types.

3 Transforming the dataset

We will now perform feature engineering and create a new feature called petal area (petal length * petal width), and will do the same for the sepal.

df['sepal_area'] = df['sepal length (cm)'] * df['sepal width (cm)']
df['petal_area'] = df['petal length (cm)'] * df['petal width (cm)']

Finally, let’s new information by binning the sepal length into 3 categories (short, medium and long)

df['sepal_length_bin'] = pd.cut(df['sepal length (cm)'], bins=3, labels=["short", "medium", "long"])
df
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) sepal_area petal_area sepal_length_bin
0 5.1 3.5 1.4 0.2 17.85 0.28 short
1 4.9 3.0 1.4 0.2 14.70 0.28 short
2 4.7 3.2 1.3 0.2 15.04 0.26 short
3 4.6 3.1 1.5 0.2 14.26 0.30 short
4 5.0 3.6 1.4 0.2 18.00 0.28 short
... ... ... ... ... ... ... ...
145 6.7 3.0 5.2 2.3 20.10 11.96 medium
146 6.3 2.5 5.0 1.9 15.75 9.50 medium
147 6.5 3.0 5.2 2.0 19.50 10.40 medium
148 6.2 3.4 5.4 2.3 21.08 12.42 medium
149 5.9 3.0 5.1 1.8 17.70 9.18 medium

150 rows × 7 columns

4 Computing summary statistics

Now, we can extract summary statistics of the species “setosa” and compare it to another species

# Map targets to species names and add them to a new column 
df['species'] = iris.target_names[iris.target] 
# Display first few rows
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) sepal_area petal_area sepal_length_bin species
0 5.1 3.5 1.4 0.2 17.85 0.28 short setosa
1 4.9 3.0 1.4 0.2 14.70 0.28 short setosa
2 4.7 3.2 1.3 0.2 15.04 0.26 short setosa
3 4.6 3.1 1.5 0.2 14.26 0.30 short setosa
4 5.0 3.6 1.4 0.2 18.00 0.28 short setosa 
# Select setosa 
df_setosa = df[df['species'] == "setosa"]
summary_stats = df_setosa.describe() 

# Display summary statistics
print(summary_stats)
       sepal length (cm)  sepal width (cm)  petal length (cm)  \
count           50.00000         50.000000          50.000000   
mean             5.00600          3.428000           1.462000   
std              0.35249          0.379064           0.173664   
min              4.30000          2.300000           1.000000   
25%              4.80000          3.200000           1.400000   
50%              5.00000          3.400000           1.500000   
75%              5.20000          3.675000           1.575000   
max              5.80000          4.400000           1.900000   

       petal width (cm)  sepal_area  petal_area  
count         50.000000   50.000000   50.000000  
mean           0.246000   17.257800    0.365600  
std            0.105386    2.933775    0.181155  
min            0.100000   10.350000    0.110000  
25%            0.200000   15.040000    0.280000  
50%            0.200000   17.170000    0.300000  
75%            0.300000   19.155000    0.420000  
max            0.600000   25.080000    0.960000